Under the patronage of:

Journal Metrics


Impact factor (2022): 2.1

5.4
2023CiteScore
 
75th percentile
Powered by  Scopus


More about CiteScore


Source Normalized Impact per Paper (SNIP): 0.474


SCImago Journal Rank (SJR): 0.377

 
 

Application of Statistical and Artificial Intelligence Techniques for Medium-Term Electrical Energy Forecasting: A Case Study for a Regional Hospital

DOWNLOAD FULL TEXT PDF
Original scientific paper

Journal of Sustainable Development of Energy, Water and Environment Systems
Volume 8, Issue 3, September 2020, pp 520-536
DOI: https://doi.org/10.13044/j.sdewes.d7.0306
Oğuzhan Timur1, Kasım Zor1 , Özgür Çelik1, Ahmet Teke1, Turgay İbrikçi2
1 Department of Electrical and Electronics Engineering, Çukurova University, Balcalı Mah. Mithat Özsan Bul., 01330, Sarıçam, Adana, Turkey
2 Department of Electrical and Electronics Engineering, Çukurova University, Balcalı Mah, Mithat Özsan Bul., 01330, Sarıçam, Adana, Turkey

Abstract

Electrical energy forecasting is crucial for efficient, reliable, and economic operations of hospitals due to serving 365 days a year, 24/7, and they require round-the-clock energy. An accurate prediction of energy consumption is particularly required for energy management, maintenance scheduling, and future renewable investment planning of large facilities. The main objective of this study is to forecast electrical energy demand by performing and comparing well-known techniques, which are frequently applied to short-term electrical energy forecasting problem in the literature, such as multiple linear regression as a statistical technique and artificial intelligence techniques including artificial neural networks containing multilayer perceptron neural networks and radial basis function networks, and support vector machines through a case study of a regional hospital in the medium-term horizon. In this study, a state-of-the-art literature review of medium-term electrical energy forecasting, data set information, fundamentals of statistical and artificial intelligence techniques, analyses for aforementioned methodologies, and the obtained results are described meticulously. Consequently, support vector machines model with a Gaussian kernel has the best validation performance, and the study revealed that seasonality has a dominant influence on forecasting performance. Hence heating, ventilation, and air-conditioning systems cover the major part of electrical energy consumption of the regional hospital. Besides historical electrical energy consumption, outdoor mean temperature and calendar variables play a significant role in achieving accurate results. Furthermore, the study also unveiled that the number of patients is steady over the years with only small deviations and have no significant influence on medium-term electrical energy forecasting.

Keywords: Electrical energy forecasting, Medium-term, Multiple linear regression, Artificial neural networks, Support vector machines, Hospital.

Creative Commons License
Views (in 2024): 584 | Downloads (in 2024): 255
Total views: 4213 | Total downloads: 1773
INTRODUCTION

Recently, accurate energy forecasting has become more of an issue for regional and national grids according to privatisation and deregulation of electric power system [1]. Precise energy forecasting models are requisite for devising and enhancement of the electric power systems [2]. However, it is complicated to forecast the consumed energy amount, because of the affecting factors consisting of climatological factors, social activities, and seasonal factors. Climatological factors depend on temperature and humidity, social factors imply human social activities consisting of work, school, and entertainment influencing the energy consumption, seasonal factors then contain seasonal climate change and annual load growth [3].

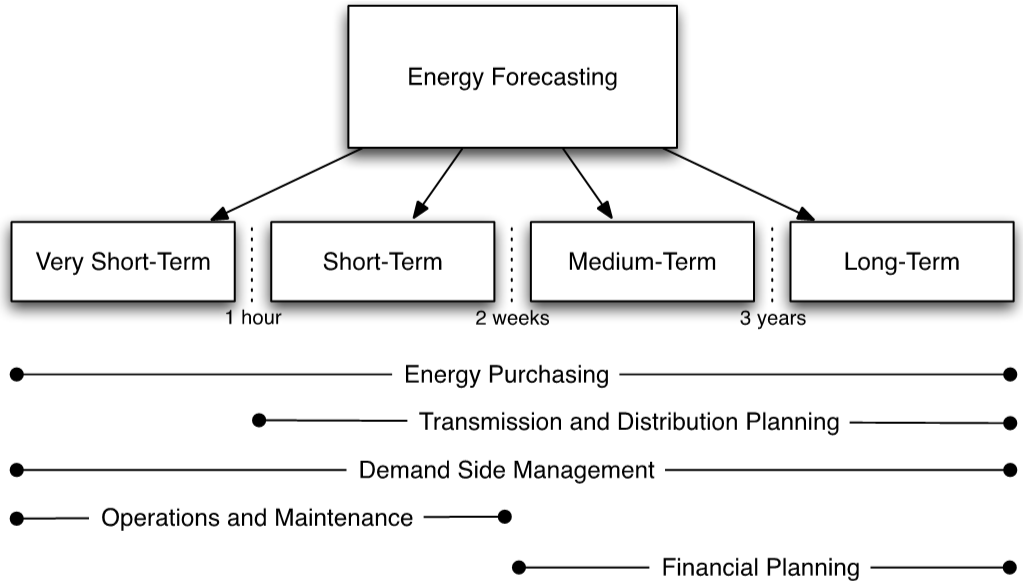
According to time horizon, there are four categories of electrical Energy Forecasting (EF):

  • Long-Term Electrical Energy Forecasting (LTEF), among 3-year and 50-year energy consumption is predicted;

  • If the forecast ranges from 2 weeks to 3-year, then it is considered as Medium-Term Electrical Energy Forecasting (MTEF);

  • Short-Term Electrical Energy Forecasting (STEF) refers to hour, day, or week ahead predictions;

  • Very Short-Term Electrical Energy Forecasting (VSTEF) which includes few minutes to an hour ahead forecasting of energy consumption [4].

LTEF is utilised for the long-term power system planning in accordance with the future energy demand and energy policy of a country [5]. MTEF is being used for the efficient operation and maintenance of the large facilities in the power system [6]. MTEF is especially interesting for companies and large state facilities operating in a deregulated environment, as it provides them valuable insights on the market need of energy, maintenance schedule, fuel supplies, and occasional needs for further investments related to renewable energy technologies [7], [8]. VSTEF and STEF play a crucial role in optimum unit commitment, control of spinning reserve, and evaluation of sales or purchase contracts between several companies [9], [10]. EF applications and classification are illustrated in Figure 1.

Energy forecasting applications and classification [11]

Statistical and Artificial Intelligence (AI) techniques are broadly used for energy forecasting applications. In the state-of-the-art literature, widely utilised statistical methods are time series analysis and regression methods. Under ordinary daily circumstances, statistical techniques have good performances, but they are not updated over time, hence they cannot yield satisfying consequences by the reasons of climatological, economic, or sociological variations. Therefore, AI techniques have accomplished significance in decreasing prediction errors. There are several AI techniques used for EF such as genetic algorithms, particle swarm optimisation, fuzzy logic, Artificial Neural Networks (ANN) and Support Vector Machines (SVM) based models. Furthermore, hybrid techniques contain more than one statistical or AI technique, or two of them together [12]. In the assumption of time series models, the current and future electrical energy consumption is a function of the historical energy consumption [13].

In the literature, Yu et al. [14] presented a large-scale study with 5,000 household meters on the performance of different forecasting methods containing the Autoregressive Integrated Moving Average (ARIMA), Holt-Winters, and ridge regression. De Oliveira and Oliveira [15] applied a combination approach of Bootstrap aggregating (Bagging) strategies and time series forecasting methods in order to predict monthly electrical energy consumption of different countries under two cases. Bennett et al. [16] identified the significant variables that affect residential low voltage network and developed next-day-energy-use and peak demand forecast models by utilising a hybrid model consisting of ARIMA with exogenous variables and neural networks for a transformer that distributes electric power to 128 residential customers in Brisbane, Australia. Qiu et al. [17] proposed an ensemble method composed of empirical mode decomposition and deep learning algorithms and applied on electric load demand data sets from Australian Energy Market Operator by comparing with nine benchmark methods. Han et al. [18] enhanced deep networks containing time-dependency convolutional neural networks and cycle-based long short-term memory to improve the forecasting performance of STEF and MTEF with a little payload of computational complexity. Zhang et al. [19] utilised the energy data collected for a period of one year for a building in a university campus in Singapore in order to forecast both half-hourly and daily electrical energy consumption by using weighted Support Vector Regression (SVR) with differential evolution algorithm. Gonzalez et al. [20] suggested a new functional forecasting method that attempts to generalise the standard seasonal autoregressive moving average with exogenous input model (ARMAX) to the L2 Hilbert space. Multiple linear regression techniques are also embroidered in the literature for residential electric energy demand forecasting. For instance, Verdejo et al. [21] reviewed the principal statistical linear parametric methods and implemented four of them to analyse real measure data from Chilean systems. Sarduy et al. [22] presented linear and nonlinear models to forecast the peak load of a campus of the University of Sao Paulo in order to choose the best one for generalisation. Goia and Gustavsen [23] carried out energy performance assessment of a semi-integrated Photovoltaic (PV) system in a zero-emission building through periodic linear regression method. Yukseltan et al. [24] developed an hourly demand forecasting method for Turkey on annual, weekly, and daily horizons by using a linear model. Ertugrul [25] performed a novel recurrent extreme learning machines approach to forecast electric load. Pino-Mejias et al. [26] tried to develop and compare linear regression models and ANN to predict the electrical energy consumption and other demands of office buildings in Chile. Rahman et al. [27] presented a recurrent neural network model to make medium-to-long-term predictions for commercial and residential buildings. Wei et al. [28] aimed at conducting a comprehensive review of the prevailing data-driven approaches and their applications to prediction and classification for building energy analysis under different patterns and granularities. Xu et al. [29] established an improved SVM algorithm with immune algorithm and fruit fly optimisation algorithm for parameter optimisation to predict short-term distributed generation load.

More specifically, studies in EF literature for hospitals or healthcare facilities are very limited and expressed as follows. Chen et al. [30] proposed STEF of air-conditioners of a hospital by using ANN for three scenarios. Morinigo-Sotelo et al. [31] presented STEF by using Multilayer Perceptron (MLP) with a sigmoid activation function for a hospital in Castile and Leon region of Spain. Bagnasco et al. [32] performed a-day-ahead STEF by using ANN for both a large university hospital located in Rome and the Cellini medical clinic of Turin [33]. Guillen-Garcia et al. [34] presented a methodology for VSTEF in a hospital in Castile and Leon region of Spain considering harmonics, inter-harmonics, and power quality disturbances. Damrongsak et al. [35] analysed the factor impacts on the energy usage of 14 hospitals in Thailand by executing Multiple Linear Regression (MLR) for MTEF. Gordillo-Orquera et al. [36] performed MTEF in a hospital and primary care centre in Fuenlabrada, Madrid for a 1-year horizon by using multivariate analysis.

In this study, an application of MLR, ANN including MLP neural networks and Radial Basis Function (RBF) networks, and SVM for MTEF of a regional hospital in Adana, Turkey is performed. After introduction, hospital information, data set, fundamentals of statistical and AI techniques, and evaluation criteria are thoroughly presented under the section of materials and methods. Significant results and discussion of the study are given in the results and discussion section. Finally, consequences of the study are summarised in the conclusion section.

Motivation

In Turkey, hospitals are seeking for renewable energy investment opportunities such as installation of a PV system to supply electricity as a reliable alternative to the grid and to sell excess electrical energy to the grid with an advantageous tariff price containing incentives (from 13.3 USDc/kWh up to 20 USDc/kWh in case of using domestically manufactured equipment [37]).

The hospitals are also planning to install tri-generation plants (so called CCHP plant which stands for combined cooling, heat, and power plant) fuelled by natural gas due to a directive [38] by Republic of Turkey Ministry of Health which states that hospitals equipped with more than 200 beds and spanning over 20,000 m2 of closed area shall install either co-generation (so called CHP which stands for combined heat and power) or tri-generation plant in order to supply their own energy demands for improving energy efficiency in health facilities [39], [40].

Before installing the mentioned plants for generating electricity to hospitals operating in a deregulated environment, MTEF, which is implemented by statistical and AI techniques, is an essential tool which provides monitoring electrical energy demand, finding base and peak loads, making viable decisions for the selection of the optimal capacity rating for both a PV system and a tri-generation plant, and enhancing energy management quality.
Contribution

The main contributions of this study are detailed as follows.

MLR, MLP neural networks, RBF networks, and SVM are well-known statistical and AI techniques which are broadly used in the literature for STEF problem [41]. The first and the most important contribution of this study is to apply those techniques to MTEF problem of a regional hospital and to compare the performances of those techniques under identical constraints.

Secondly, the statistical and AI techniques are validated by using real-time data obtained from a regional hospital having diversified load characteristics, and the study unveiled that seasonality has a dominant influence on MTEF performance of the hospital wherein Heating, Ventilation, and Air-Conditioning (HVAC) systems constitute the major part of electrical energy consumption. In addition to historical electrical energy consumption, outdoor mean temperature and calendar variable play a significant role in achieving accurate results. Furthermore, studies in the MTEF literature are limited especially for real-time applications, and this study is considered to fill the gap in the EF literature.

Thirdly, MTEF is performed for a 5-year period using statistical and AI techniques with the same validation method which is a 10-fold cross validation. Applying the same validation method reveals the genuine performance of the statistical and AI techniques for a better comparison in terms of coefficient of determination (R2), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and run time.

Consequently, an introduction with the state-of-the-art literature, data set information with elucidate graphs, definition of the statistical and AI techniques with an explanatory table that addresses advantages and disadvantages of the techniques, evaluation criteria with mathematical formulae, and significant results containing a graph for predicted and actual target values are expressed and demonstrated throughout the study in detail in order to assist prospective researchers in the field.
MATERIALS AND METHODS

The regional hospital is a pioneer health institution and serves unceasingly a region in the Southern Turkey that covers the area containing Adana, Mersin, Hatay, Osmaniye, Kahramanmaraş, Gaziantep, and Kilis. Thus, it has continuous demands to supply electricity for one emergency service, forty-two polyclinics, twelve intensive care units, twenty-three operating rooms, forty-three clinical services, five laboratories, one radiology unit, nuclear medicine, one blood centre, one burn unit, one sterilisation unit, and one pharmacy, laundries, kitchens, and a morgue. The hospital has 1,200 beds and serves more than 3,000 patients per day with over 3,000 personnel and has an installed transformer capacity around 18 MVA [42]. Aerial view of the regional hospital is illustrated in Figure 2.

Aerial view of the regional hospital
Data set

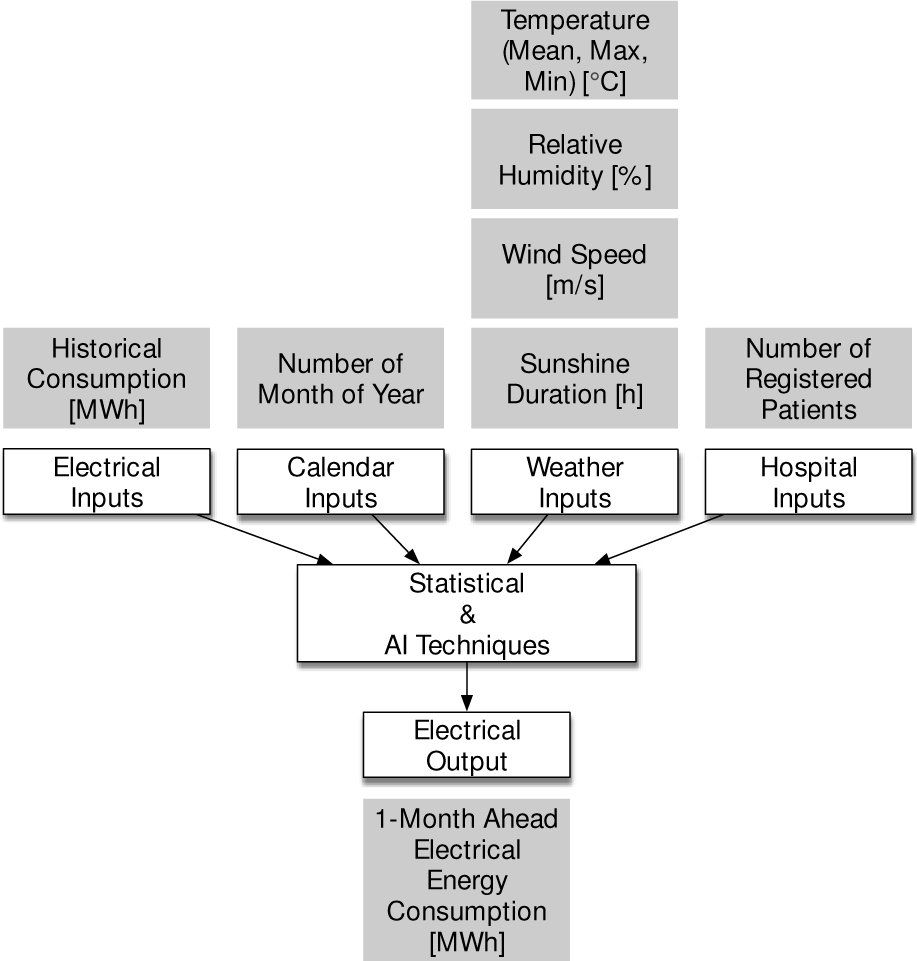
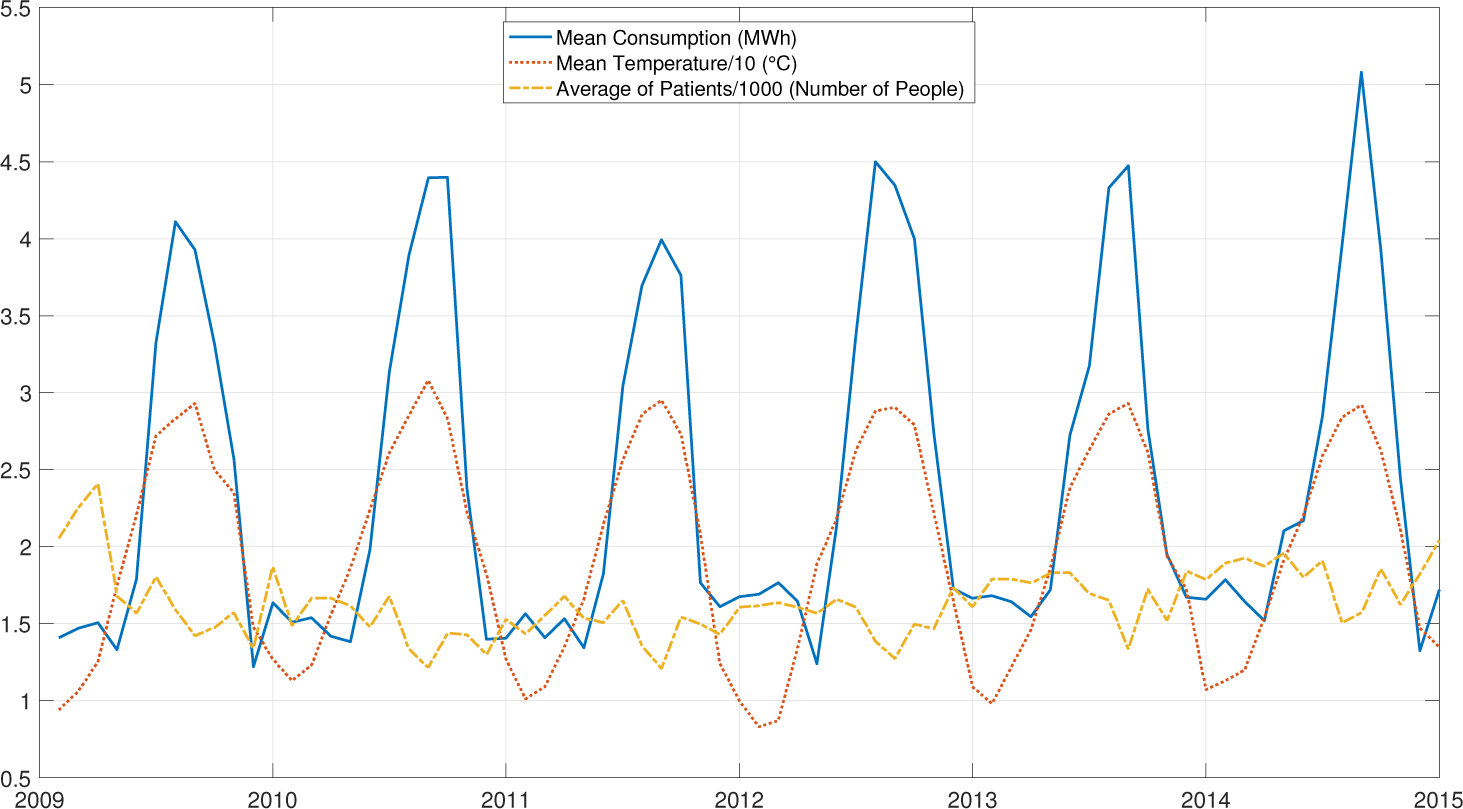
Input and output variables of data set are shown in Figure 3. In Figure 4, monthly mean electrical energy consumption per hour, monthly mean temperature, and monthly mean average of patients per day are illustrated to reflect hospital’s retrospective data. Monthly mean electrical energy consumption per hour varies between 1.221 MWh and 5.078 MWh, monthly mean temperature changes from 8.3 °C to 30.8 °C, and monthly average of patients per day ranges from 1,209.06 patients to 2,407.48 patients. In order to show different kinds of data in the same graph, the values belonging to monthly mean temperature and monthly average of patients per day are divided by 10 and 1,000, respectively. Figure 4 reveals that the number of patients is steady over the years with small deviations and having no significant influence on forecasting, while seasonality draws attention for both electrical energy consumption and temperature simultaneously.

Flowchart of input and output variables

Hospital data are obtained for the time period between 2009 and 2015. The obtained data are daily, however, they are converted to monthly mean data due to performing MTEF.

Illustration of hospital’s data between 2009 and 2015
Statistical and Artificial Intelligence techniques

In this study, statistical technique as MLR and AI techniques including ANN and SVM are applied to MTEF. Ordinarily, these techniques are commonly used for STEF in the literature, and the reason behind the selection of those techniques is to implement the techniques to MTEF, to observe their performances, and to discuss the results whether they are applicable to MTEF or not.

Comparison table of statistical and AI techniques that contains pros and cons of each technique individually is indicated in Table 1.

Comparison table of statistical and AI techniques [11], [41]

Technique Model Pros Cons
Statistical MLR Easy to calculateFastHas good interpretabilityRequires less memory Its nature of assuming a linear relationship between dependent and independent variablesOversimplifies real world problemsCan cause severe multicollinearityProne to outliers
AI ANN Needs less formal statistical trainingImplicitly detects complex relationships between dependent and independent variablesDetects all possible interactions between predictor variablesHas access to multiple training algorithms Its nature of being a backboxHas greater computational costTends to overfittingThe empirical nature of the model development
SVM Avoids overfitting by regularisation parameterKernel trickCan be defined by an optimisation problem having no local minima and there are efficient methods for solution of it The first and biggest limitation depends on the choice of kernelThe second limitation in speed and size for both in training and testing stagesSignificantly slow in the testing stage
Multiple Linear Regression.

In the field of electrical energy consumption modelling, the goal of MLR as a statistical technique is to formalise the relationship among various explanatory variables such as weather and calendar information, and a dependent variable which is the amount of electrical energy demand as a linear function in order to predict the consumed energy amount as closely as possible [43]. The model using MLR is expressed as:

y=β0+β1x1+β2x2+…+βnxn+e (1)

where y is the consumed energy, xi is the value of independent variables, ßi is the regression parameter with respect to xi, and e represents error [44]. In MLR, the error term corresponds to a set of random variables, independent and identically distributed with a Gaussian distribution having zero mean [43].

The main reasons of the selection of MLR in this study as a statistical technique are its simplicity for understanding, its ease of use, and its faster operation in comparison with other techniques.
Artificial Neural Networks.

The simplest and smallest unit of ANN is an artificial neuron which has the capability of managing complex behaviours between the operative neurons and weight parameters [45]. In general, the fundamental topology of ANN is represented by a feed-forward MLP neural network which is constituted by three types of neuron layers, namely input layer, hidden layer, and output layer:

y^=b0+∑h=1Hbhgδ0i+∑i=1Iδhipi (2)

where I represents the number inputs pi and H is the number of hidden nodes in the network. The weights ω = (b,δ), where b = [b1, ..., bH] and δ = [δ11, ..., δH1], are for the hidden and output layer sequentially. b0 and δ0i are the biases of each node, and the transfer function g(·) may be nonlinear and is usually either the sigmoid logistic or the hyperbolic tangent function [46].

Recently, RBF networks have been considered as a promising alternative to MLP neural networks owing to their broad spectrum of applications and quicker learning ability. In comparison with traditional sigmoidal MLP neural networks, RBF networks have minimal interaction between RBF units, because each RBF unit is typically influenced by smaller portions of input patterns [47]. In RBF networks, merely one hidden layer is in existence and neurons of the hidden layer contain radial basis activation functions. Hence, output of an RBF network is tantamount to the weighted summation of the responses of the hidden neurons and can be explained as:

yj=∑i=1nωijφix−ci+b0j,   j=1,2,…,n (3)

where the number of nodes in the hidden layer is n, input vector is x, the centre of the ith hidden node is ci, the weight of ith node of the hidden layer is ωij, the radial basis function with ci being its centre is φi, and the bias of the j node of output layer is b0j. The mapping from the input layer to the hidden layer is nonlinear, while it is linear from the hidden layer to the output layer. Herein, the radial basis function is a Gaussian function and input-to-centre distance is designated by utilising simple Euclidean distance as indicated below:

φix=exp−x−ci2σ2 (4)

where σ < 0 is a predefined spread value of the function. It should be noted that three key parameters are decided in RBF networks which are spread, centres, and inter-network weights [48].

The fundamental reasons behind the selection of ANN in this study as an AI technique are its fully approximation for any complex nonlinear relationship, its high-speed search in determining the ideal number of hidden layers and the optimal number of neurons within the layers, and capable of learning and adapting to unknown or uncertain systems.
Support Vector Machines.

SVM is an AI technique for binary classification problems. With an extension to SVM, the technique can also be applied to regression problems (i.e. SVR) for function estimation [49]. SVR is utilised to constitute a quite flat function f(x), which is a linear regression function, that has the capability to get the nearest vector representing the real output with a tolerance ε indicating error term. EF has nonlinear solutions just as most problems encountered on the Earth, hence input data are mapped into a higher-dimensional space by using SVR in order to find out probable linearities for training data, and linear regression technique can be applied to the consequent space:

fx=ω×φx+b (5)

where φ(x) is a function used for mapping from nonlinear space to linear space and b corresponds to the bias [50]. In order to guarantee the flatness of f(x), a function having a minimum norm value of ||ω||2 should be obtained for each residual possessing a value smaller than ε. In practice, a cost can be defined for residuals that are not smaller than or equal to ε, because such function may not be obtained. For this optimisation problem, formulation of nonlinear ε-insensitive SVR (ε-SVR) is as follows:

minω,b12ω2+C∑i=1lξi+ξi* (6)

s.t.yi−fx≤ε+ξifx−yi≤ε+ξi*ξi,ξi*≥0 (7)

where the penalty imposed on observations that lie outside the ε margin is controlled by C and shown by ξi and ξi*. Dual optimisation problem of ε-SVR can be acquired by introducing a Lagrangian function with multipliers αj and αj*. Each instance must conform to Karush-Kuhn-Tucker (KKT) conditions as well. Lagrangian multipliers for all instances throughout the margin are zero. Instances having multipliers, that are not equal to zero, are support vectors. In that case, the function f(x) is stated as:

fxi=∑j=1lαj−αj*Kxi,xj+b (8)

where K(xi, xj) is a nonlinear kernel function [51]. Linear, sigmoid, polynomial, and Gaussian RBF are universally utilised kernels. Due to its simplicity and computational efficiency over the years, RBF kernel has been qualified as one of the best kernels [52]. RBF kernel function is expressed as:

Kxi,xj=exp−xi−xj22σ2=exp−γ×xi−xj2 (9)

where xi and xj are input instances, σ2 is variance, and ||xi – xj||2 can be described as the squared Euclidean distance among two instances [51].

Moreover, cost (C) controls the SVR model’s empirical risk degree, gamma (γ) controls the Gaussian function width, and epsilon (ε) controls the ε-insensitive zone’s width sequentially. For the performance of SVR models, C, γ, and ε parameters should be well-determined in order to have a more accurate ε-SVR model [19].

In this study, SVM is chosen as an AI technique due to its ability to be performed with less parameters, its kernel trick which simplifies nonlinear relationships into linear ones by mapping, and its capability in improving generalisation performance.
Evaluation criteria

Normalisation process is essentially performed to eliminate the units of different data types in the data set, to maintain data integrity for decreasing execution time and occupying less memory, and to compare performances of heterogeneous data in a similar manner. In order to have a data distribution between 0 and 1 for each column vector representing different data type, the following formula can be applied for ymin = 0 and ymax = 1:

xnorm=ymax−ymin×x−xminxmax−xmin+ymin (10)

where x is a column vector, xmin and xmax correspond to minimum and maximum values of x, while ymin and ymax are boundaries for distribution and xnorm represents a normalised column vector converted from x, respectively [53].

Before evaluation, normalised data have to be de-normalised to calculate performance metrics which can only be compared between models whose errors are measured in the similar units such as RMSE. De-normalisation formula is the same as normalisation formula, but ymax and ymin represent the minimum and maximum known values of the previously normalised column vector x.

In order to evaluate the performances of different statistical and AI techniques, R2, RMSE, and MAPE are employed in this study. R2 corresponds to the coefficient of determination which is the proportion of the variance in the dependent variable that can be predicted from the independent variables [54]. RMSE is a quadratic scoring rule for the square root of the variance which also represents the average of the root forecasting error squares [55]. However, there is no precise criterion for an optimum value of RMSE, hence it is based on the scales of the measured variables and the size of the sample. RMSE can be only compared among models whose errors are measured in the same units [56]. On the other hand, MAPE performance metric does not depend on the magnitude of the unit of measurement. If the MAPE is small, then the model is accurate. MAPE is the most widely used error measure in energy forecasting [57]. Formulae of R2, RMSE, and MAPE are as follows:

R2=1−∑i=1nyi−y^i2∑i=1nyi−y¯2 (11)

RMSE=∑i=1nyi−y^i2n (12)

MAPE%=1n∑i=1nyi−y^iyi×100 (13)

where yi is actual or measured output, y^i is predicted output, y¯ is mean of yi, and n indicates the number of observations.
RESULTS AND DISCUSSION

All analyses throughout this study are performed in MATLAB R2017b in a Windows based personal computer that has Intel Core i5-3330 CPU at 3.00GHz, 16GB DDR3 RAM, and 1TB HDD.

In all statistical and AI techniques, 10-fold cross validation method is employed for validating the models by training on 9-fold and testing on 1-fold in order to eliminate the bias and this process is implemented 10 times in a row. In Table 2, average values of the result of 10 iterations for cross validation are shown.

MLR model is chosen to present the most widely used method because of its simplicity, and training MLR model is the fastest in comparison with others owing to requiring less memory for implementation as a statistical method.

In MLP neural networks, a search is performed from 2 to 20 neurons in order to find the optimal neuron number in the hidden layer, and the optimal neuron number is found as 2 because of having the minimum residual variance at that neuron number. Logistic activation functions are used for the hidden layer and linear activation functions are utilised for the output layer. Scaled Conjugate Gradient (SCG) back propagation algorithm is employed for the training method of MLP neural networks to optimise the weight values.

Performance comparison of the applied techniques

Technique Model R2 [%] RMSE [MWh] MAPE [%] Run time [s]
Statistical MLR 85.77 0.41 15.79 0.13
AI MLP 93.61 0.27 9.52 0.55
RBF 90.66 0.33 11.83 4.04
SVM 94.90 0.24 8.89 2.28

In RBF networks, different types of radial basis functions can be used, but the most common is the Gaussian function that is also utilised in this study. RBF networks can be evaluated as a specialised topology under MLP neural networks with a single hidden layer. Number of neurons in the hidden layer is changed from 2 to 50 in order to reach the optimal neuron number which is computed as 21. Minimum spread, maximum spread, minimum lambda, and maximum lambda are found as 0.023, 396.052, 0.155, and 9.206 seriatim.

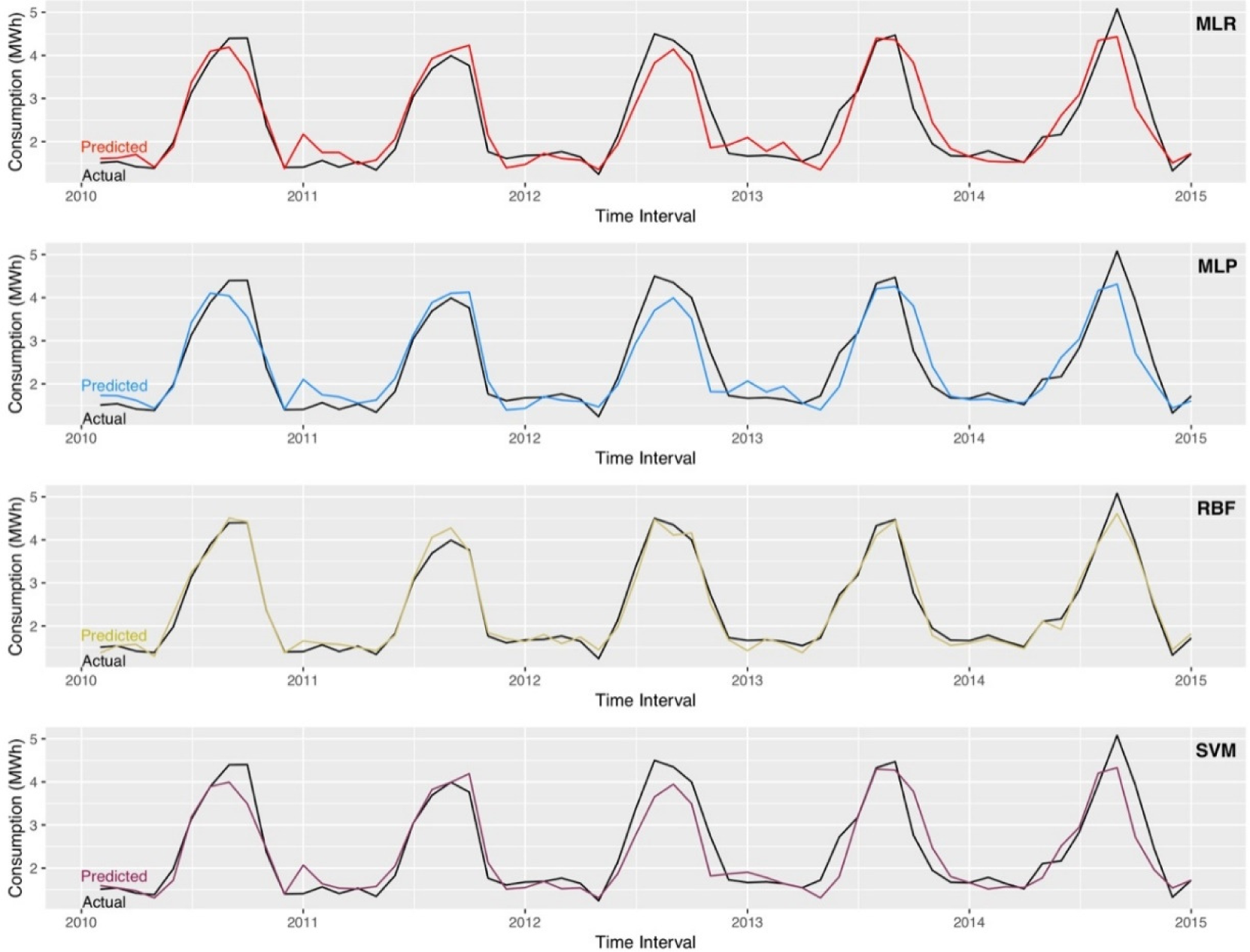
ε-SVR is used with Gaussian kernel function for SVM model. A grid search is performed for model parameters between 0.1 and 5,000 for C, 0.001 and 50 for γ, and 0.0001 and 100 for ε in order to overcome the generalisation problem by minimising Mean Squared Error (MSE), number of support vectors used by the model is 40, and the C, γ and ε parameters are respectively found as 36.0105, 0.4356, and 0.001. Graphs containing predicted and actual target values for each statistical and AI technique are given in Figure 5.

According to the results indicated in Table 2, R2 values for all models are generally over 85%. In addition, the best performances of MAPE are 8.89% for SVM, 9.52% for MLP neural networks, 11.83% for RBF networks, and 15.79% for MLR models. RMSE performances are also the same with MAPE rankings. Run times of models are 0.13 s for MLR, 0.55 s for MLP neural networks, 2.28 s for SVM, and 4.04 s for RBF networks. In addition to those, having the same variance in input data for all models, residual variances after the model fits are sequenced as 0.06 for SVM, 0.07 for MLP, 0.11 for RBF, and 0.17 for MLR. The results exhibit that the best approach for MTEF was obtained by using SVM model having a MAPE of 8.89%. In other respects, it is obvious that MAPE of MLP neural networks model is close to SVM model’s performance, but it should be emphasised that run time of MLP neural networks model is almost one fourth of SVM model’s run time.

Moreover, when all of the results are interpreted together for MTEF, SVM model is the best choice if the minimum error is primary target. MLP model is an excellent alternative when the minimum error and run time are taken into account together. Unlikely, RBF model does not seem as a suitable match with the data set used in this study and it is not recommended for MTEF applications. MLR model is suggested to use for MTEF if run time is the top priority for consideration.

Furthermore, when relative importance of input variables is deeply investigated, it should be noted that beside historical electrical energy consumption, outdoor mean temperature and calendar variable play a significant role in achieving accurate results. Seasonality draws attention because of the fact that HVAC systems cover the major part of electrical energy consumption of the regional hospital. The number of patients is steady for years with small deviations and have no significant influence on MTEF.

Predicted and actual target value graphs for statistical and AI techniques [58], [59]
CONCLUSIONS

MTEF is a considerable tool that ensures monitoring electrical energy consumption, identifying base and peak loads, determining the optimal capacity rating for installing feasible power plants, and improving energy management quality in hospitals.

In this study, statistical and AI techniques named as MLR, ANN containing MLP neural networks and RBF networks, and SVM, which are frequently utilised in the literature for STEF, are applied to real-time data obtained from a regional hospital in Adana, Turkey in order to perform MTEF under identical constraints and to fill the gap in the EF literature. The EF of the upcoming month is carried out by the models which take the impacts of various input parameters named as historical electrical energy consumption, outdoor mean temperature, outdoor maximum temperature, outdoor minimum temperature, sunshine duration, wind speed, relative humidity, number of registered patients, and number of months into account.

The results indicate that presented statistical and AI techniques provide reasonable accuracy in forecasting monthly mean electrical energy consumption. However, when the obtained results are investigated, SVM model provides a successful convergence. In addition, MLP model’s performance is not only close to the SVM model, but also MLP model’s run time is one fourth of run time of the SVM model. Moreover, the case study revealed that the historical electrical energy consumption, outdoor mean temperature and calendar variable are the most determinative predictors among the utilised input parameters due to the dominant influence of seasonality because of the fact that HVAC systems cover the major part of electrical energy consumption of the regional hospital.

Consequently, SVM and MLP neural networks give superior results for the EF problem. Also, this study unveiled that the SVM, MLP, and MLR models can be implemented not only to STEF applications, but also MTEF applications for future studies.
ACKNOWLEDGMENT

This work was supported by the Scientific Research Project Unit of Çukurova University [grant number FYL-2014-2351]. The authors are grateful for the research data provided by Turkish State Meteorological Service and the regional hospital. The authors also would like to thank the anonymous reviewers for their valuable comments and suggestions.
NOMENCLATURE
MAPE mean absolute percentage error [%]
MSE mean squared error [MWh2]
RMSE root mean squared error [MWh]
R2 coefficient of determination [%]
Abbreviations
AI Artificial Intelligence
ANN Artificial Neural Networks
ARIMA Autoregressive Moving Average
ARMAX Autoregressive Moving Average with Exogenous Input Model
CCHP Combined Cooling, Heat, and Power
CHP Combined Heat and Power
CPU Central Processing Unit
DDR Double Data Rate
EF Electrical Energy Forecasting
HDD Hard Disk Drive
HVAC Heating, Ventilation, and Air-Conditioning
KKT Karush-Kuhn-Tucker
LTEF Long-Term Electrical Energy Forecasting
MLP Multilayer Perceptron
MLR Multiple Linear Regression
MTEF Medium-Term Electrical Energy Forecasting
PV Photovoltaic
RAM Random Access Memory
RBF Radial Basis Function
SCG Scaled Conjugate Gradient
STEF Short-Term Electrical Energy Forecasting
SVM Support Vector Machines
SVR Support Vector Regression
US The United States
VSTEF Very Short-Term Electrical Energy Forecasting
REFERENCES
  1. Allouhi A., Fouih Y., Kousksou T., Jamil A., Zeraouli Y., Mourad Y.Energy Consumption and Efficiency in Buildings: Current Status and Future Trends, 2015,
  2. Hong W.Electric Load Forecasting by Support Vector Model, 2009,
  3. Barakati S., Rafiei S., Gharaveisi A.Short-Term Load Forecasting Using Mixed Lazy Learning Method, 2015,
  4. Hong T., Fan S.Probabilistic Electric Load Forecasting: A Tutorial Review, 2016,
  5. Spiegel T.Impact of Renewable Energy Expansion to the Balancing Energy Demand of Differential Balancing Groups, 2018,
  6. Bekteshi S., Kabashi S., Ahmetaj S., Slaus I., Zidansek A., Podrimqaku K., Kastrati S.Dynamic Modeling of Kosovo’s Electricity Supply-Demand, Gaseous Emissions and Air Pollution, 2015,
  7. Kaboli S., Fallahpour A., Selvaraj J., Rahim N.Long-Term Electrical Energy Consumption Formulating and Forecasting via Optimized Gene Expression Programming, 2017,
  8. Gerse A.Future Generation Adequacy of the Hungarian Power System with Increasing Share of Renewable Energy Resources, 2015,
  9. Raza M., Khosravi A.A Review on Artificial Intelligence Based Load Demand Forecasting Techniques for Smart Grid and Buildings, 2015,
  10. Bennett C., Stewart R., Lu J.Forecasting Low Voltage Distribution Network Demand Profiles Using a Pattern Recognition Based Expert System, 2014,
  11. Zor K., Timur O., Teke A.A State-Of-The-Art Review of Artificial Intelligence Techniques for Short-Term Electric Load Forecasting, 2017,
  12. Esener I., Yuksel T., Kurban M.Short-Term Load Forecasting Without Meteorological Data Using AI-Based Structures, 2015,
  13. Chae Y., Horesh R., Hwang Y., Lee Y.Artificial Neural Network Model for Forecasting Sub-Hourly Electricity Usage in Commercial Buildings, 2016,
  14. Yu C., Mirowski P., Ho T.A Sparse Coding Approach to Household Electricity Demand Forecasting in Smart Grids, 2017,
  15. de Oliveira E., Oliveira F.Forecasting Mid-Long Term Electric Energy Consumption Through Bagging ARIMA and Exponential Smoothing Methods, 2018,
  16. Bennett C., Stewart R., Lu J.Autoregressive with Exogenous Variables and Neural Network Short-Term Load Forecast Models for Residential Low Voltage Distribution Networks, 2014,
  17. Qiu X., Ren Y., Suganthan P., Amaratunga G.Empirical Mode Decomposition Based Ensemble Deep Learning for Load Demand Time Series Forecasting, 2017,
  18. Han L., Peng Y., Li Y., Yong B., Zhou Q., Shu L.Enhanced Deep Networks for Short-Term and Medium-Term Load Forecasting, 2019,
  19. Zhang F., Deb C., Lee S., Yang J., Shah K.Time Series Forecasting for Building Energy Consumption Using Weighted Support Vector Regression with Differential Evolution Optimization Technique, 2016,
  20. Gonzalez J., Roque A., Perez E.Forecasting Functional Time Series With a New Hilbertian ARMAX Model: Application to Electricity Price Forecasting, 2018,
  21. Verdejo H., Awerkin A., Becker C., Olguin G.Statistic Linear Parametric Techniques for Residential Electric Energy Demand Forecasting: A Review and an Implementation to Chile, 2017,
  22. Sarduy J., Santo K., Saidel M.Linear and Non-Linear Methods for Prediction of Peak Load at University of Sao Paulo, 2016,
  23. Goia F., Gustavsen A.Energy Performance Assessment of a Semi-Integrated PV System in a Zero Emission Building Through Periodic Linear Regression Method, 2017,
  24. Yukseltan E., Yucekaya A., Bilge A.Forecasting Electricity Demand for Turkey: Modeling Periodic Variations and Demand Segregation, 2017,
  25. Ertugrul O.Forecasting Electricity Load by a Novel Recurrent Extreme Learning Machines Approach, 2016,
  26. Pino-Mejias R., Perez-Fargallo A., Rubio-Bellido C., Pulido-Arcas J.Comparison of Linear Regression and Artificial Neural Networks Models to Predict Heating and Cooling Energy Demand, Energy Consumption and CO2 Emissions, 2017,
  27. Rahman A., Srikumar V., Smith A.Predicting Electricity Consumption for Commercial and Residential Buildings Using Deep Recurrent Neural Networks, 2018,
  28. Wei Y., Zhang X., Shi Y., Xia L., Pan S., Wu J., Han M., Zhao X.A Review of Data-Driven Approaches for Prediction and Classification of Building Energy Consumption, 2018,
  29. Xu X., Niu D., Wang Q., Wang P., Wu D.Intelligent Forecasting Model for Regional Power Grid With Distributed Generation, 2017,
  30. Chen C., Shih S., Hu S., Short-Term Electricity Forecasting of Air-Conditioners of Hospital Using Artificial Neural Networks, Proceedings of IEEE/PES Transmission Distribution Conference Exposition: Asia and Pacific, 2005
  31. Morinigo-Sotelo D., Duque-Perez O., Garcia-Escudero L., Fernandez-Temprano M., Fraile-Llorente P., Riesco-Sanz M., Zorita-Lamadrid A., Short-Term Hourly Load Forecasting of a Hospital Using an Artificial Neural Network, Proceedings of International Conference on Renewable Energies and Power Quality, 2011
  32. Bagnasco A., Saviozzi M., Silvestro F., Vinci A., Grillo S., Zennaro E., Artificial Neural Network Application to Load Forecasting in a Large Hospital Facility, Proceedings of International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), 2014
  33. Bagnasco A., Fresi F., Saviozzi M., Silvestro F., Vinci A.Electrical Consumption Forecasting in Hospital Facilities: An Application Case, 2015,
  34. Guillen-Garcia E., Zorita-Lamadrid A., Duque-Perez O., Morales-Velazquez L., Osornio-Rios R., Romero-Troncoso R.Power Consumption Analysis of Electrical Installations at Healthcare Facility, 2017,
  35. Damrongsak D., Wongsapai W., Thinate N.Factor Impacts and Target Setting of Energy Consumption in Thailand’s Hospital Building, 2018,
  36. Gordillo-Orquera R., Lopez-Ramos L., Munoz-Romero S., Iglesias-Casarrubios P., Arcos-Aviles D., Marques A., Rojo-Alvarez J.Analyzing and Forecasting Electrical Load Consumption in Healthcare Buildings, 2018,
  37. Law Regarding to the Use of Renewable Energy Sources for Electrical Energy Production, Version 3, http://eskiweb.epdk.org.tr/TR/Dokuman/6777
  38. Teksan A., Kocar G., Eryasar A., Aytav E., Investigation of Benefits of Co-Generation/Tri-Generation Applications in Hospitals Through a Case Study, Proceedings of 5th National Electrical Installation Congress and Exhibition, 2017
  39. Teke A., Timur O.Assessing the Energy Efficiency Improvement Potentials of HVAC Systems Considering Economic and Environmental Aspects at the Hospitals, 2014,
  40. Teke A., Zor K., Timur O.A Simple Methodology for Capacity Sizing of Cogeneration and Trigeneration Plants in Hospitals: A Case Study for a University Hospital, 2015,
  41. Wang Q., Li S., Li R.Forecasting Energy Demand in China and India: Using Single-Linear, Hybrid-Linear, and Non-Linear Time Series Forecast Techniques, 2018,
  42. Timur O., Design and Implementation of a Wireless Sensor Network for Energy Monitoring, Analysis and Management in Smart Buildings, Ph.D. Thesis, 2018
  43. Hong T., Gui M., Baran M., Willis H., Modeling and Forecasting Hourly Electric Load by Multiple Linear Regression With Interactions, Proceedings of IEEE PES General Meeting, 2010
  44. Amral N., Ozveren C., King D.Short Term Load Forecasting Using Multiple Linear Regression, 2007,
  45. Yildirim H., Celik O., Teke A., Barutcu B.Estimating Daily Global Solar Radiation With Graphical User Interface in Eastern Mediterranean Region of Turkey, 2018,
  46. Barrow D., Kourentzes N.The Impact of Special Days in Call Arrivals Forecasting: A Neural Network Approach to Modelling Special Days, 2018,
  47. Yu H., Xie T., Paszczynski S., Wilamowski B.Advantages of Radial Basis Function Networks for Dynamic System Design, 2011,
  48. Hossain M., Ong Z., Ismail Z., Khoo S.A Comparative Study of Vibrational Response Based Impact Force Localization and Quantification Using Radial Basis Function Network and Multilayer Perceptron, 2017,
  49. Avsar E.Dimensionality Reduction for Predicting CO Conversion in Water Gas Shift Reaction over Pt-Based Catalysts Using Support Vector Regression Models, 2017,
  50. Zendehboudi A., Baseer M., Saidur R.Application of Support Vector Machine Models for Forecasting Solar and Wind Energy Resources: A Review, 2018,
  51. Vrablecova P., Ezzeddine A., Rozinajova V., Sarik S., Sangaiah A.Smart Grid Load Forecasting Using Online Support Vector Regression, 2018,
  52. Yaslan Y., Bican B.Empirical Mode Decomposition Based Denoising Method With Support Vector Regression for Time Series Prediction: A Case Study for Electricity Load Forecasting, 2017,
  53. He Y., Zheng Y.Short-Term Power Load Probability Density Forecasting Based on Yeo-Johnson Transformation Quantile Regression and Gaussian Kernel Function, 2018,
  54. Celik O., Teke A., Yildirim H.The Optimized Artificial Neural Network Model with Levenberg-Marquardt Algorithm for Global Solar Radiation Estimation in Eastern Mediterranean Region of Turkey, 2016,
  55. Akay M., Abasikeles I.Predicting the Performance Measures of an Optical Distributed Shared Memory Multiprocessor by Using Support Vector Regression, 2010,
  56. Salkind N., 2010,
  57. Zor K., Timur O., Celik O., Yildirim H., Teke A., Interpretation of Error Calculation Methods in the Context of Energy Forecasting, Proceedings of 12th Conference on Sustainable Development of Energy, Water and Environment Systems (SDEWES), 2017
  58. , 2018, http://www.rstudio.com
  59. Wickham H., , ggplot2: Elegant Graphics for Data Analysis, 2016

DBG